My Mathematics Undergraduate Degree: A Comprehensive Breakdown
I recently completed studying for a Bachelor of Mathematics and a Bachelor of Computer Science. Here I will go through a full breakdown of my mathematics degree. This is part one of a two part series, where in the second part I will go through my Computer Science degree. In this post I will go through and reflect on all mathematics, statistics and physics courses I have taken including what I learned, what I liked, what I didn’t like and the textbook I used if applicable. All textbooks I have read is available on my goodreads.
Semester 1 2021

 Since this was during the COVID-19 pandemic, I should mention that the university was largely open to students during this time with several closures lasting a couple of weeks at most. Lectures were to be held online through Zoom for the entire year while other classroom activities such as practicals and workshops could go ahead with some restrictions on class size. Since my last year of high school in 2020, I have utilised the time tracking technique through Toggl Track software. I started with the Pomodoro technique with a ratio of 25 minutes work and 5 minutes break. This really helped me form my study habits. The first thing to notice for my first semester of university is the lack of mathematics course. This is because I started out as a computer science and physics student through a double degree program studying a Bachelor of Computer Science and a Bachelor of Science. At the start, computer science was my main focus with an interest in science and physics in particular. At the time not taking a maths course made sense since I was interested in different areas. But with the benefit of hindsight I should have prioritised taking the first maths course in this semester as to be completely aligned with the natural progression of courses. Also I would then be able to take the advanced version of some maths courses which are only run once per year which I did not have the opportunity to do.
Since this was during the COVID-19 pandemic, I should mention that the university was largely open to students during this time with several closures lasting a couple of weeks at most. Lectures were to be held online through Zoom for the entire year while other classroom activities such as practicals and workshops could go ahead with some restrictions on class size. Since my last year of high school in 2020, I have utilised the time tracking technique through Toggl Track software. I started with the Pomodoro technique with a ratio of 25 minutes work and 5 minutes break. This really helped me form my study habits. The first thing to notice for my first semester of university is the lack of mathematics course. This is because I started out as a computer science and physics student through a double degree program studying a Bachelor of Computer Science and a Bachelor of Science. At the start, computer science was my main focus with an interest in science and physics in particular. At the time not taking a maths course made sense since I was interested in different areas. But with the benefit of hindsight I should have prioritised taking the first maths course in this semester as to be completely aligned with the natural progression of courses. Also I would then be able to take the advanced version of some maths courses which are only run once per year which I did not have the opportunity to do.
With a recommended study time of 10-12 hours per week per course and with 13 weeks making up a semester discounting mid-semester break, SWOTVAC and exam period, almost all of the courses I took in my first semester fell below this region which does indicate a lack of maturity and experience in this regard which is true. Over the course of the semester and accounting for all courses taken, I spent over 25 hours on a five minute pomodoro break. The miscellaneous project was an attempt to record my time participating in psort but I quickly abandoned because it was not working for me. It would have been interesting to find a reliable method to have the data available over the years.
Theory and Practice in Science (SCIE1000): This is a basic introduction to university courses and made for a smooth transition between high school and university. The main point of the course was to introduce mathematical and computational methods in order to answer questions in science. It essentially acted as an introduction to scientific computing by developing mathematical models and solving with computers. There was also a module on philosophy and ethics in science. Generally the content introduced basic mathematical or computational concepts with a large number of examples provided from many different aspects of science (physics, engineering, chemistry, biology, ecology, genetics etc.). This was the first time I had seen programming used to solve scientific problems rather than a problem in software engineering.
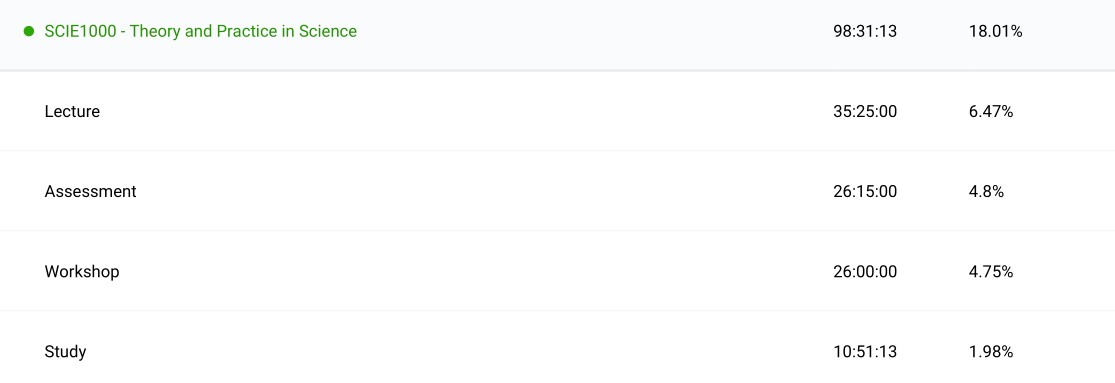
Mechanics and Thermal Physics (PHYS1001): As evident by the name, the first physics course deals with newtonian mechanics for the first two-thirds and the last third is dedicated to thermal mechanics. This was quite a large course in volume of content and set the precedent for what was expected when studying physics. There were weekly quizzes prior to and during workshops, five pieces of laboratory assessment, although this was entirely contained to within the practical sessions so no lab reports yet, three theory assessments and fortnightly practice problems, all before the final exam. While I am still below the recommended number of hours, my personal study hours are much higher here. This consists of reading the textbook, taking and organising notes and studying for exams. The textbook used was ‘Physics for Scientists and Engineers: A Strategic Approach’ by Randall Knight. It isn’t a bad textbook and makes an effort to adequately explain concepts and gives many examples and diagrams. But it reads like a high school textbook where the examples make up the majority of the content and not mathematical results. Having mandatory quizzes prior to the workshops did not work well for me. In my experience, I simply read the textbook in order to answer the set questions without absorbing any of the details. As a result my notes were lacklustre and usually consisted of a sentence or two of theory, some diagrams from the textbook and a quick example.
Semester 2 2021
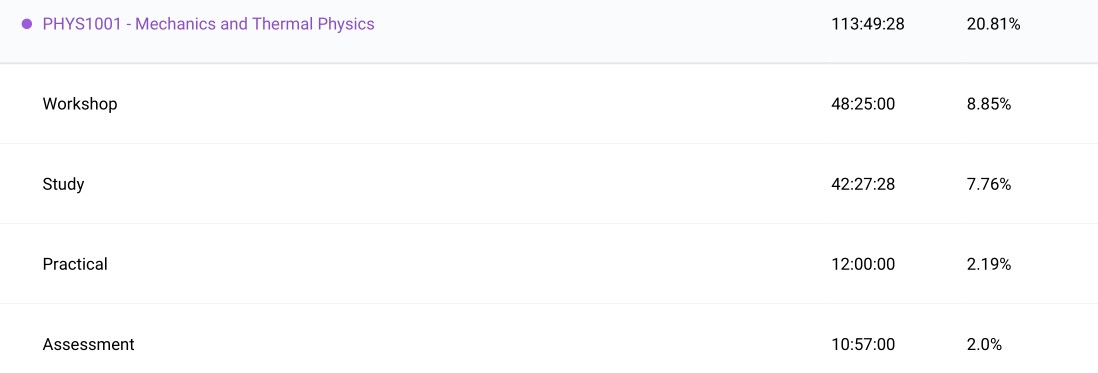
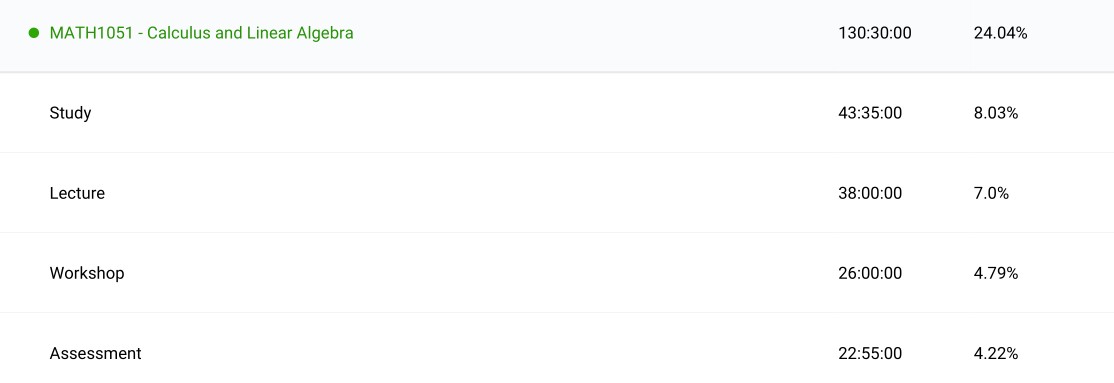
 My second semester consisted entirely of mathematics, physics and statistics courses. Also it is clear to see a step up in time devoted to study.
My second semester consisted entirely of mathematics, physics and statistics courses. Also it is clear to see a step up in time devoted to study.
Calculus & Linear Algebra I (MATH1051): The calculus section was really an extension to high school calculus, although some neat techniques were introduced. The textbook followed was ‘Calculus: Early Transcendentals’ by James Stewart and I enjoyed it. I found it useful to gain information from as it has good motivation for the topics, concise explanations that get at the point of the subject supplemented by examples and diagrams. I did not enjoy how much of the content was purely exercises to gain experience applying techniques. While necessary, it meant that I knew how to do things rather than why I would want to. For example more time was spent on series than sequences, so my takeaway was that series are an important tool in mathematics, which is not really the case relative to the importance of sequences in later areas. I think I would have enjoyed the advanced version of this course more which was more proof oriented. This course introduces MATLAB as a computational tool. This component had the same problem as the calculus where I felt like I was simply plugging away to arrive at a solution rather than learning MATLAB as a useful tool. But it was worthwhile having another tool available for use and having the experience to pick it up later. Finally, the linear algebra section was new to me. Although I was familiar with matrices and vectors, the underlying theory was novel. Although it was more application based, I appreciated seeing the theory for the first time and getting to the heart of what a vector is and why we can do what we do with matrices. By the end of the section I felt like I had not explored linear algebra nearly enough and wanted to know more about it. ‘Elementary Linear Algebra, Applications Version’ was a good starting reference.
Discrete Mathematics (MATH1061): I thoroughly enjoyed this course. This course is what set in motion my transition from physics to mathematics. This was my introduction to a proof-based course. Much of the content was directly applicable to further courses especially on the computer science side including logic, graph theory, number theory, probability and combinatorics. But it was the sections on set theory and abstract algebra that piqued my interest. Seeing mathematics broken down into a small number of axioms that generalise beyond the real numbers blew my mind. Being my first time exposed to group theory and finite fields, I could understand why this would be useful to model a problem in this way, but I could not quite grasp why it worked so elegantly. In particular constructing and showing homomorphisms and isomorphisms between abstract groups felt natural yet difficult at the same time. It was from this that I really wanted to study more of it. The textbook ‘Discrete Mathematics with Applications’ by Susanna Epp was an adequate reference for most of the content but lacked the depth I was after on group theory.
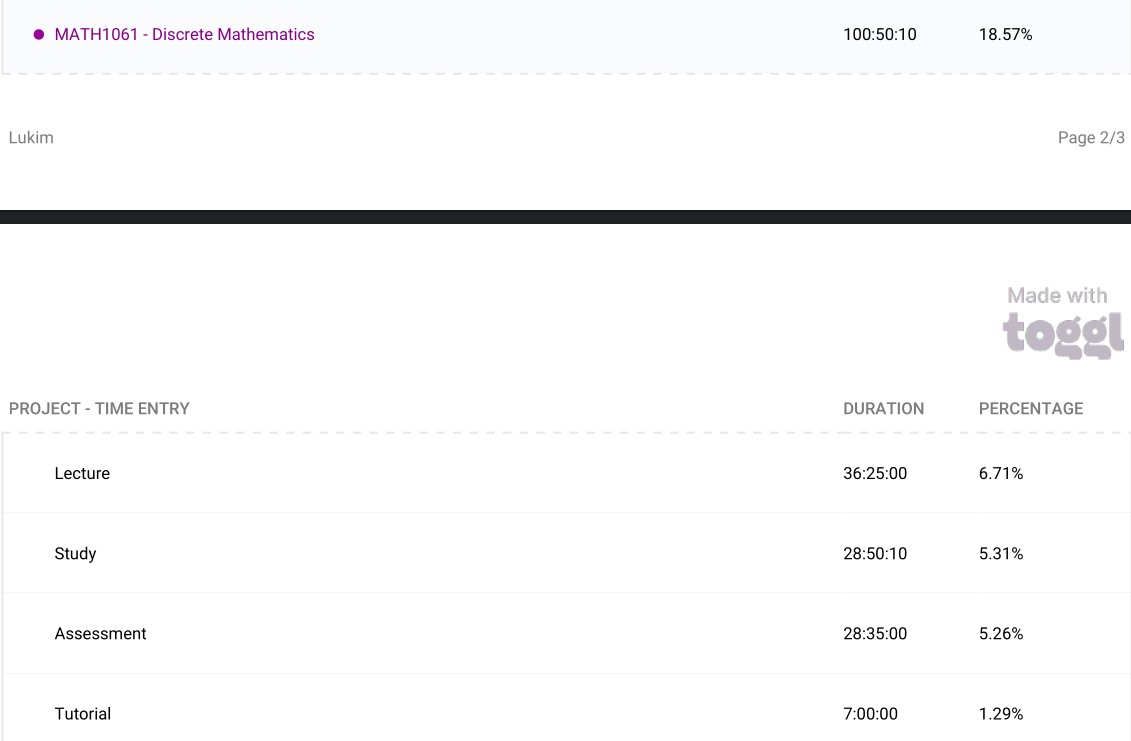
Advanced Analysis of Scientific Data (STAT1301): While advanced statistics was mandatory for mathematics program, it was optional under science program so it was a good thing that I convinced myself to take the advanced version when presented the choice. The course struck the best balance between exploring underlying theory in a deep and meaningful way and solving problems in applications and computation from the courses I had taken so far. I belive in part it is because data is useful and easy to see its applications outside of a neatly constructed course in being able to turn raw data into useful information and draw accurate conclusions. The computation aspect was conducted in R and integrated nicely into the course structure with solid examples throughout. This course was also the first time I felt like I was doing real science where some assessment tasks included finding a modern published paper that contains some kind statistical value and running further statistical analysis or reviewing the ethics of data collection process. Overall I found this to be a useful course even if I don’t exactly love statistics as a field of study personally. ‘Modern Mathematical Statistics’ by Jay Devore was a good reference as it did a good job at explaining the theory of statistics in a concise way and showing good examples.
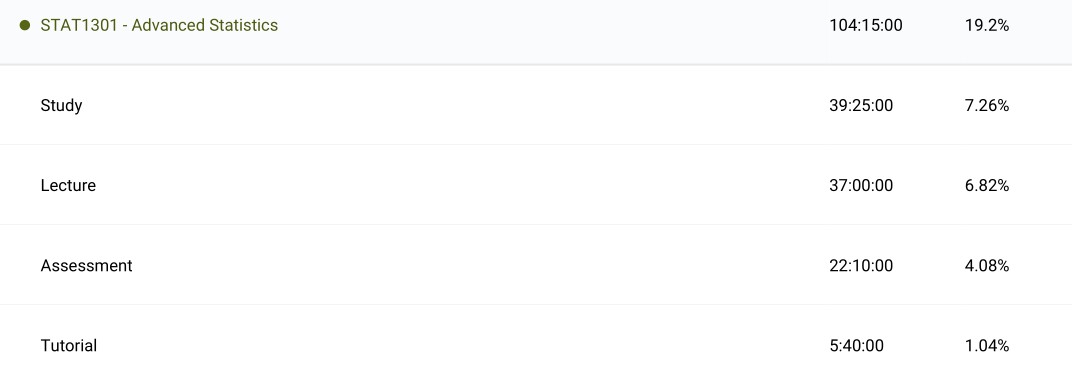
Electromagnetism and Modern Physics (PHYS1002): This course was a mild disaster for me in all honesty. I simply lacked the mathematical experience required to succeed at a high level. It generally came from the early part of the course in electromagnetism. I remember struggling with it during high school as well. The theory made sense, but I struggled to truly comprehend the actual phenomena. The optics and modern physics section was enjoyable and I did much better at those parts. The format was largely identical to PHYS1001 but now there were lab reports introduced as assessment. Overall I found the balance of workload to be much higher than that of mathematics courses. Although this was not reflected in the total hours worked, it showed in the quality of work submitted. This experience combined with passion for mathematics cemented my decision to major in mathematics instead of physics. I still enjoyed physics for the most part so I went on to complete a minor in physics where I focused primarily on quantum mechanics.
Semester 1 2022
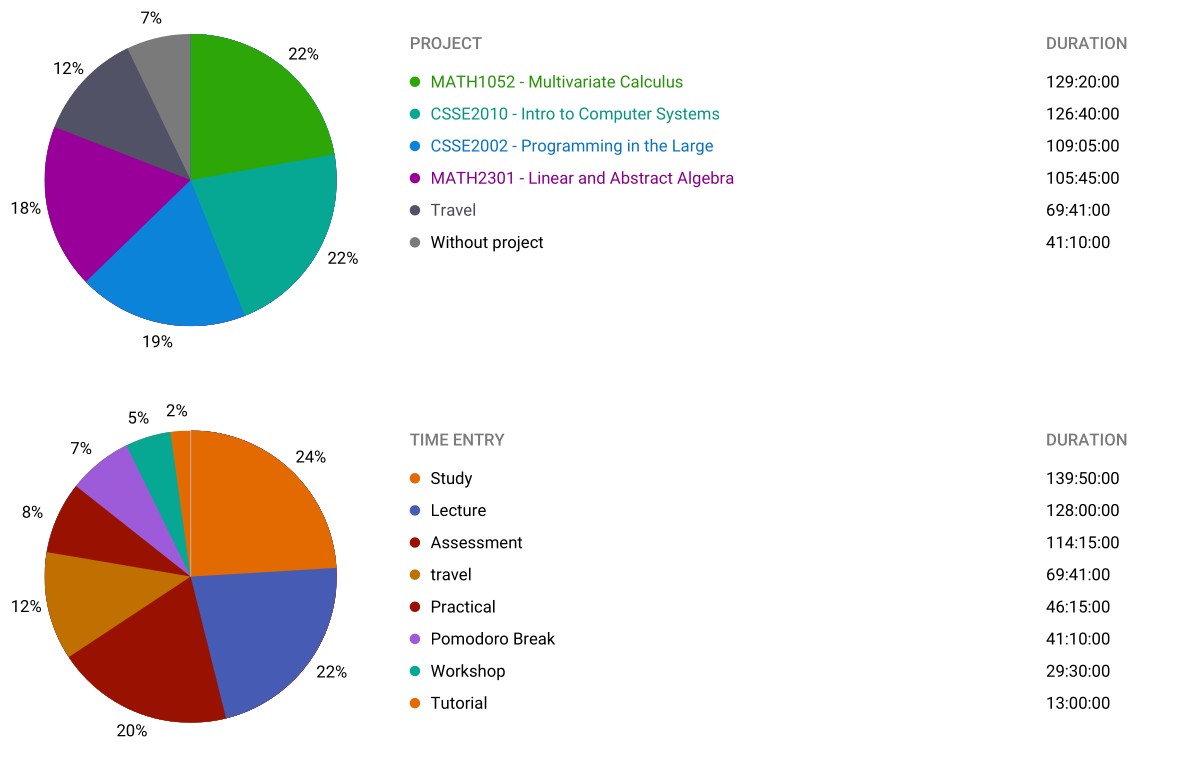 I had now officially made the switch from Bachelor of Science to Bachelor of Mathematics and I had chosen at this point to major in pure mathematics.
I had now officially made the switch from Bachelor of Science to Bachelor of Mathematics and I had chosen at this point to major in pure mathematics.
Multivariate Calculus & Ordinary Differential Equations (MATH1052): The first half of the course dealt with introducing the concept of an ODE and exploring the theory and problem-solving techniques before moving on to multivariate calculus. I found this to be an enjoyable course that exceeded my expectations. The direct applications of learned techniques were easy to comprehend which motivated the content nicely. The multivariate section also introduced ideas from geometry so all in all it was an interesting course. The MATLAB component was also good and I felt like I was getting comfortable with this new piece of software to solve scientific problems.
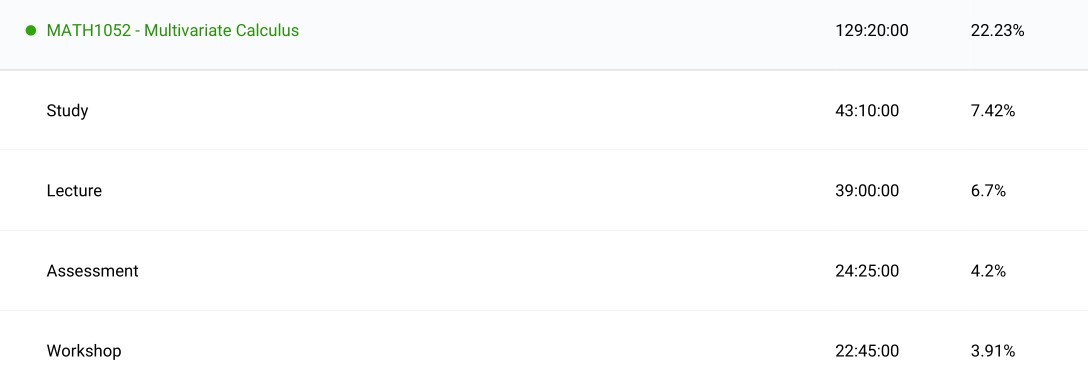
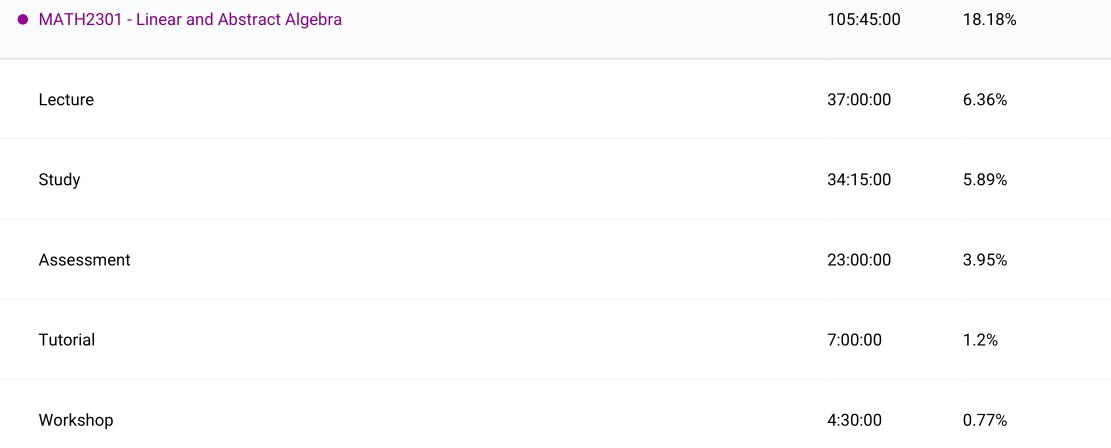
Linear & Abstract Algebra & Number Theory (MATH2301): This was the first course for me which was pure proof-based with definitions, lemmas, propositions and theorems. So it was a new way to approach mathematics which I enjoyed. I could get comfortable with the concepts of bijections, homomorphisms and isomorphisms while exploring deeper theory. I saw more examples of groups without numbers like cyclic and symmetric groups, also how functions and polynomials can make up a group too. The textbook ‘Abstract Algebra: Theory and Applications’ was the main source of literature I followed. The number theory section was fairly interesting but not an area of mathematics I was particularly interested in as a whole. ‘Elementary Number Theory’ was a good reference. The second part was purely devoted to linear algebra and only interested in the theory. I was unprepared for the depth this section would explore. This course is normally paired in conjunction with another calculus and linear algebra course which would be a good complement, but since I took math courses out of sequence by a semester, I did not get this experience. I couldn’t fully understand why we would want to do the things we do in linear algebra such as canonical forms. ‘Linear Algebra, fourth edition’ was the reference. Nevertheless I enjoyed the course and it definitely shaped the mathematics student I became.
Semester 2 2022
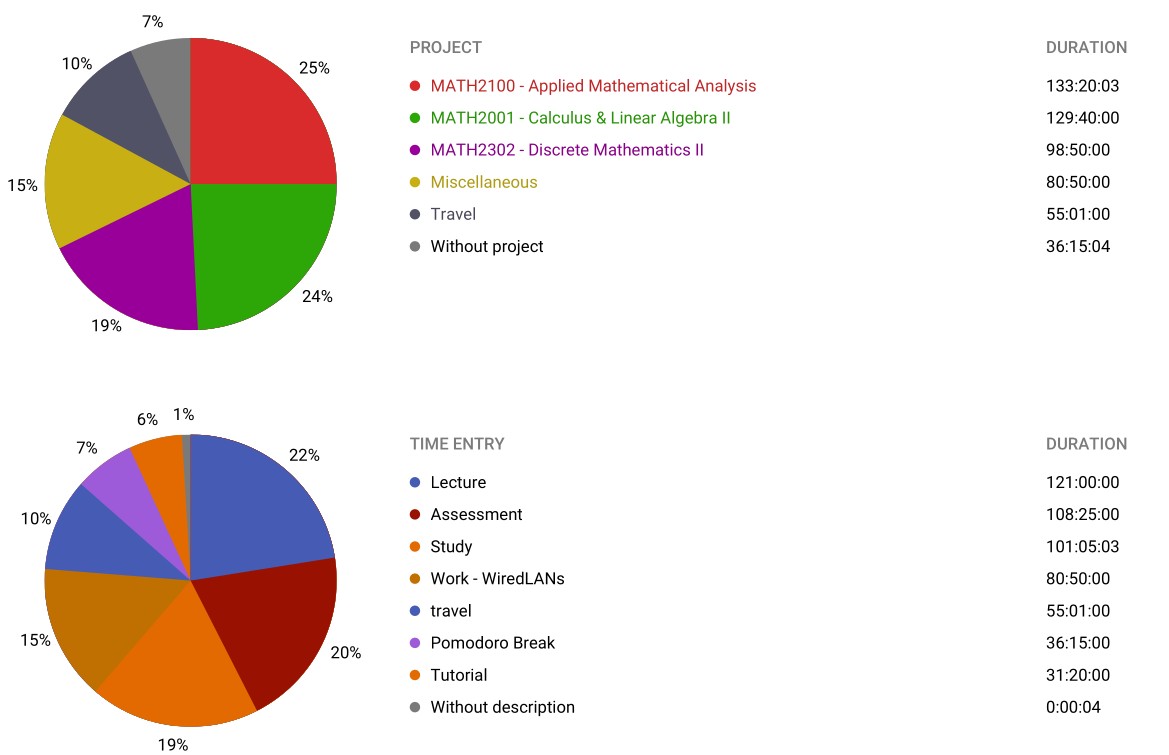 There are only three courses for this semester for I started working part time. I had enrolled in a quantum mechanics course but withdrew to be able to work. This had the effect of extending my program by another semester to a total of 4.5 years. This also was an opportunity for me to concentrate on a reduced number of courses which led to a visible increase in final grades. It was in this semester that I finally started to feel my study habits taking shape and how I was maturing as a student in mathematics
There are only three courses for this semester for I started working part time. I had enrolled in a quantum mechanics course but withdrew to be able to work. This had the effect of extending my program by another semester to a total of 4.5 years. This also was an opportunity for me to concentrate on a reduced number of courses which led to a visible increase in final grades. It was in this semester that I finally started to feel my study habits taking shape and how I was maturing as a student in mathematics
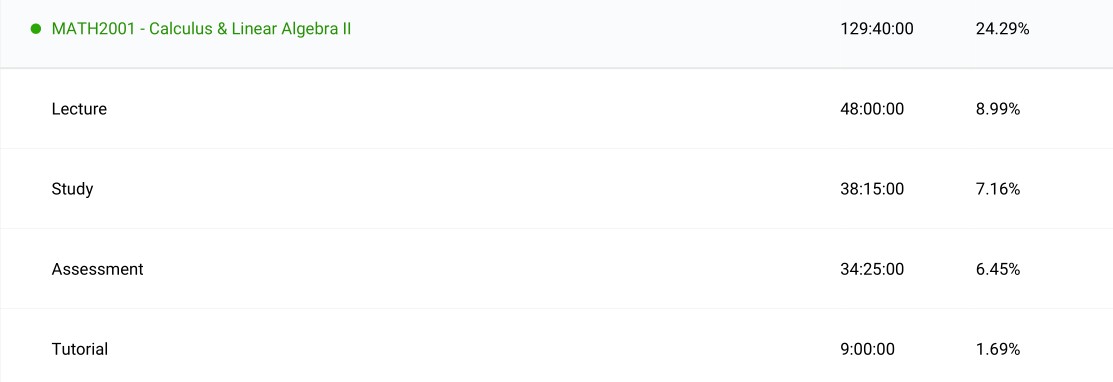
Calculus & Linear Algebra II (MATH2001): There was a lot of content in this course spanning areas of ODEs, linear algebra, multivariate and vector calculus. This course was where I really felt like I grasped the beauty and prestige in some of the theorems both in their proofs and their results. Perhaps it was familiarity with the basics of previous courses or a sign of maturity and understanding or likely a combination of both.
Applied Mathematical Analysis (MATH2100): The first half deals with ODEs yet again and the Laplace transformation while second half goes through fourier series and partial differential equations. At first I did not want to take this course as it was technically an elective but I had exhausted all other options due to program and majors but I am glad that I had to because I found it enjoyable. The textbook I used was ‘Differential Equations’ by Paul Blanchard. The first half was relatively simple now this was my third time with ODEs. The second half was very computationally heavy and the mathematics looked extremely complicated but I enjoyed solving problems by invoking techniques and utilising tricks to simplify the given problem. For this section I used ‘Fourier Series and Boundary Value Problems’ by Ruel Vance Churchill. This course was also an introduction to mathematica software which was a useful tool to have available.
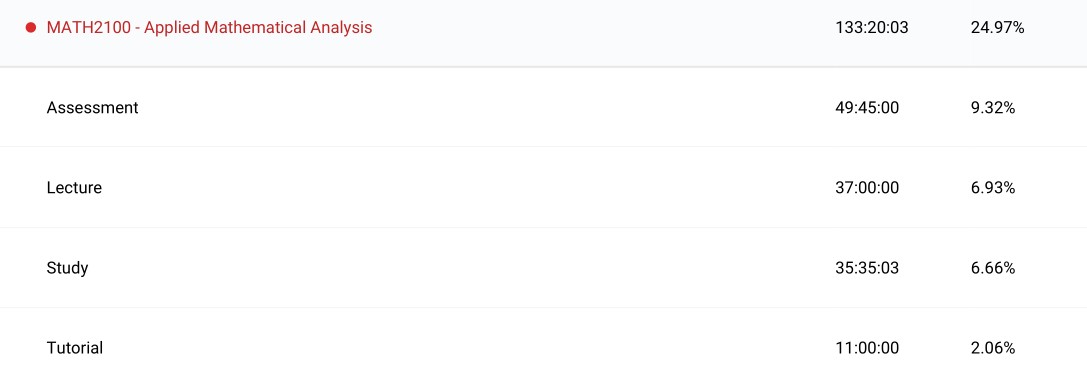
Discrete Mathematics II (MATH2302): This course actually counted towards my machine learning major as it was a prerequisite for that program. The majority of this course deals with combinatorics and graph theory as well as covering topics in design theory and elementary geometric topology. This largely fell outside my area of interests but the topics were still interesting and useful to know. Design theory, though, did not make a lot of sense to me at the time. Topics covering groups and the introduction to topology were the most valuable parts of the course to me. Although graph theory was useful when it came to algorithms. Course notes were mainly used as study material but ‘Combinatorial Mathematics’ by Douglas West was useful for majority of content. I used ‘A Guide to the Classification Theorem for Compact Surfaces’ by Jean Gallier for the topology and surfaces section.
Semester 1 2023
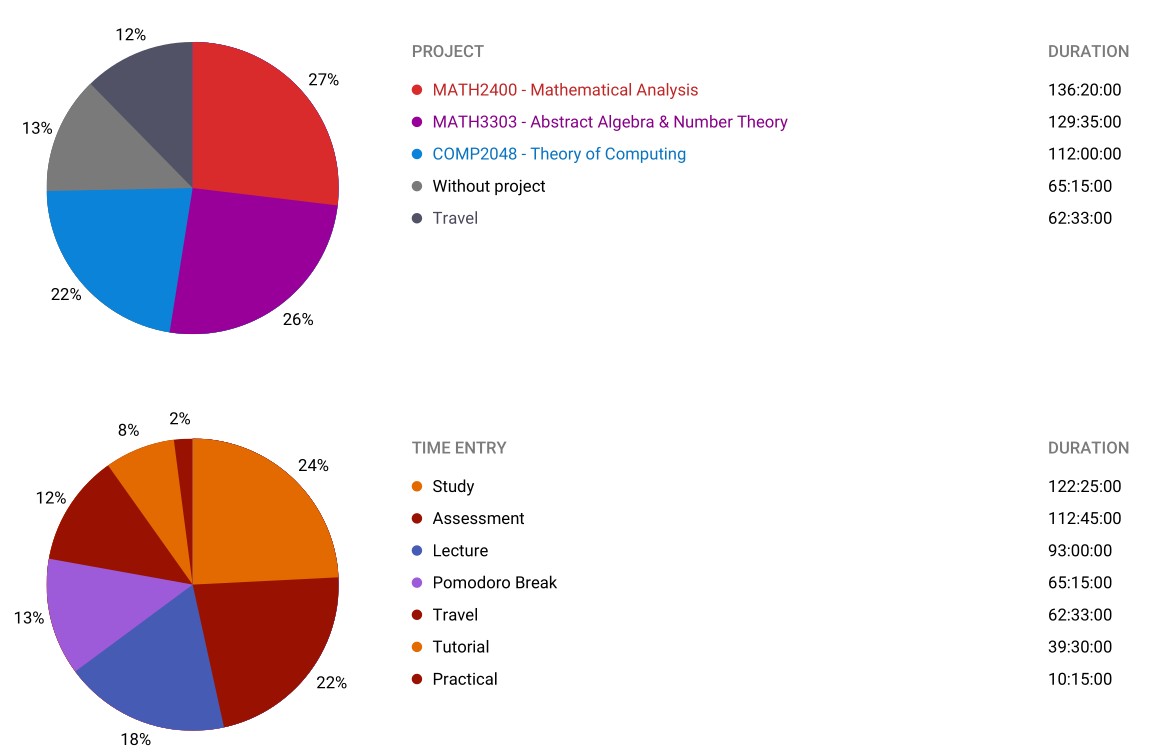 An interesting observation for this semester is the large increase in time tracked for pomodoro break. Up until now, I was using the standard 25/5 ratio recommended. It was good for forming study habits but I found it to be too short for deep work. I adopted a 45/15 ratio instead. What I found was that I was able to have many more sessions before getting tired so I could get a lot more study done this way. I eventually found that the 10 minute swing in productivity (5 minute drop in work time and 5 minute increase in break time) moving to this new ratio was unsuitable at the end of the year so I continued to make adjustments. This ratio is probably my favourite that I have worked with even if slightly suboptimal.
An interesting observation for this semester is the large increase in time tracked for pomodoro break. Up until now, I was using the standard 25/5 ratio recommended. It was good for forming study habits but I found it to be too short for deep work. I adopted a 45/15 ratio instead. What I found was that I was able to have many more sessions before getting tired so I could get a lot more study done this way. I eventually found that the 10 minute swing in productivity (5 minute drop in work time and 5 minute increase in break time) moving to this new ratio was unsuitable at the end of the year so I continued to make adjustments. This ratio is probably my favourite that I have worked with even if slightly suboptimal.
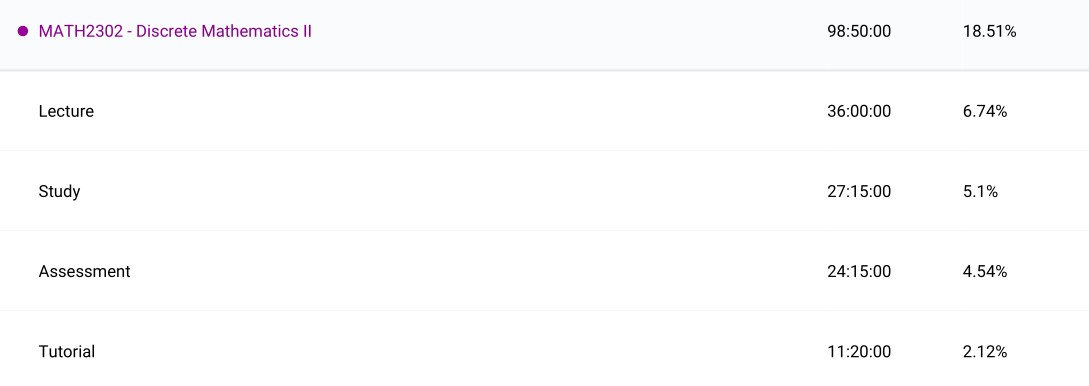
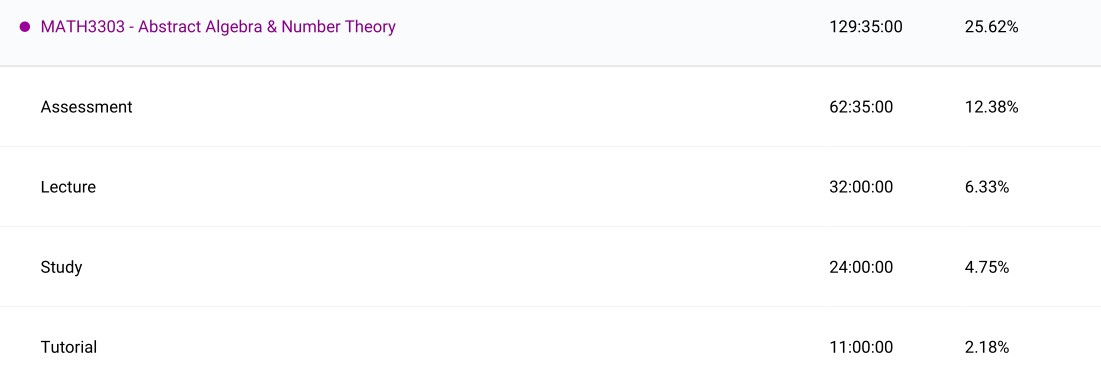
Abstract Algebra & Number Theory (MATH3303): Despite the name there was no number theory covered and it was purely an abstract algebra course which was good news to me as that is what I wanted to learn the most. Being the first third year course, it was a nice change to go deep into one area of mathematics rather than cover a broad range of topics. This course really pushed me to think like a mathematician for the first time to explore and understand deep properties of groups, rings and fields. Abstract algebra is simple in the number of axioms required to get started but it is not necessarily easy, there are many deep and important theorems and results. ‘Abstract Algebra: An Introductory Course’ by Gregory Lee was a great reference to use as well. All in all this was a fantastic course and became one of my favourites.
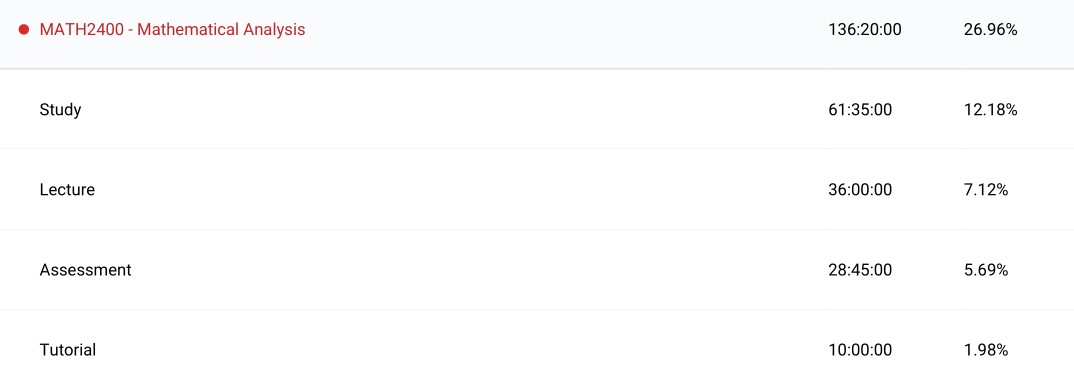
Mathematical Analysis (MATH2400): Finally after nearly three years, I was introduced thoroughly to epsilon-delta proof techniques. I did not enjoy this course to be frank. The premise made sense; to put calculus on rigorous grounding as to know exactly why we are allowed to do the things in calculus. Despite being proof-based, it still ended up being a course where exercises and methods seemed to be the key takeaway over the theorems and results. There was an advanced version of the course that, once again, I could not take which may have been better for someone like me. ‘Basic Analysis: Introduction to Real Analysis, Volume I & II’ as the main source of literature did not satisfy my appetite. Metric spaces seemed like an interesting structure that was kind of glossed over and never brought up again after the one week spent developing the theory. Since taking topology and functional analysis, I have a much greater appreciation for the notion of open sets to derive properties such as continuity and compactness. Perhaps I should return to this area in much greater detail in my own time some time in the future.
Semester 2 2023
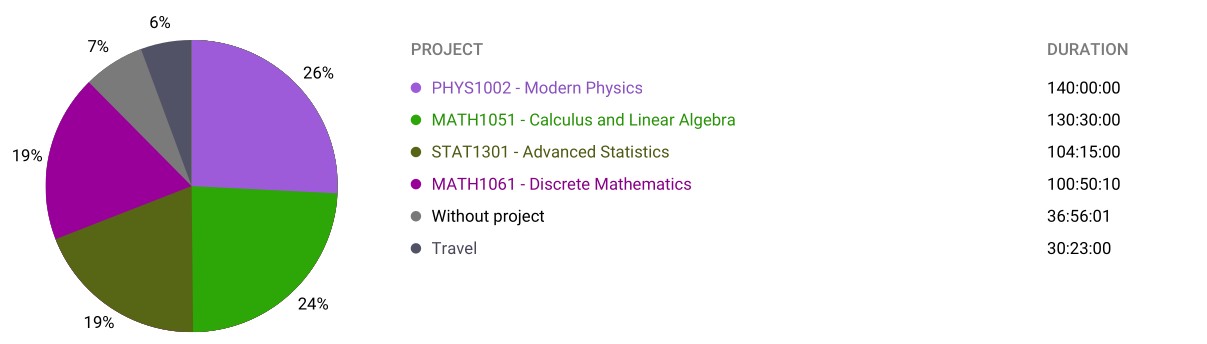
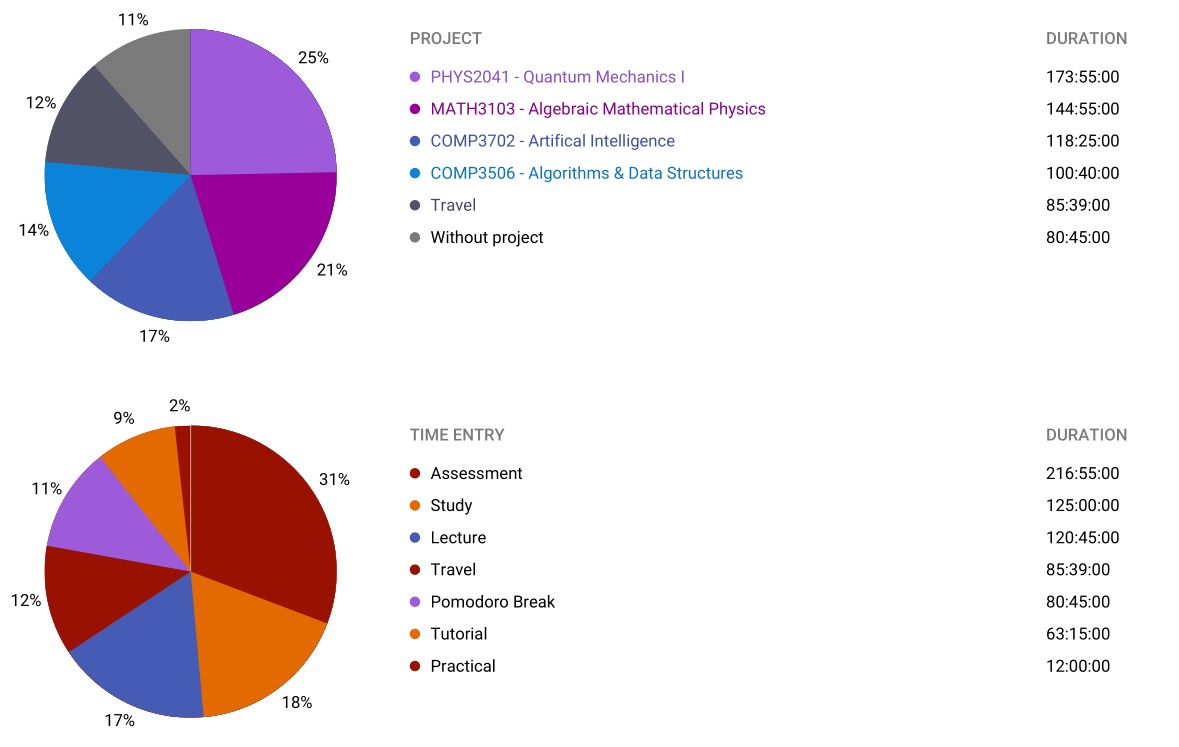 Going into this semester I had decided to switch my mathematics major from pure mathematics to mathematical physics. I felt like this made more sense to me as I was interested in what behaviour these mathematical spaces and structures could model and it connected well with my studies in quantum physics; this became the sort of mathematics most interesting to me rather than rigorous proofs of theorems offered by pure mathematics. The wagon wheels show the intensity of this semester which I believe to be, at least partly, a consequence of the longer study sessions I could put together. I had put more time into studying for quantum mechanics I than the recommended 10-12 hours per week which also shows the disparity in workload between physics and mathematics and computer science courses.
Going into this semester I had decided to switch my mathematics major from pure mathematics to mathematical physics. I felt like this made more sense to me as I was interested in what behaviour these mathematical spaces and structures could model and it connected well with my studies in quantum physics; this became the sort of mathematics most interesting to me rather than rigorous proofs of theorems offered by pure mathematics. The wagon wheels show the intensity of this semester which I believe to be, at least partly, a consequence of the longer study sessions I could put together. I had put more time into studying for quantum mechanics I than the recommended 10-12 hours per week which also shows the disparity in workload between physics and mathematics and computer science courses.
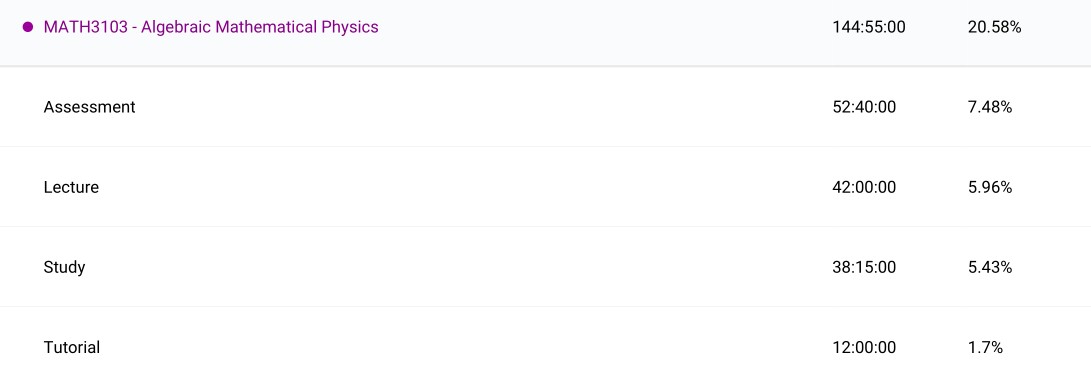
Algebraic Methods of Mathematical Physics (MATH3103): A vague name for a course in Lie algebras and representation theory, central to the mathematical physics major. I regard this course as probably the msot difficult course I had taken throughout my program. The first half dealt with the theory in a very pure way while the second offered connections to real phenomena in quantum mechanics. After taking third year abstract algebra I naively thought this would be another standard algebra course that I was used to at this point, and it started off that way. I was not prepared for how deep and complex the mathematics got. I almost regret taking this course so soon in my program and I think I would have got more out of it and enjoyed it more had I left it later so I could see the connections made between quantum mechanics and other areas of mathematics such as differential geometry and functional analysis. James Humphreys’ ‘Introduction to Lie Algebras and Representation Theory’ was an excellent source. I intend to revisit this area soon in my own studies.
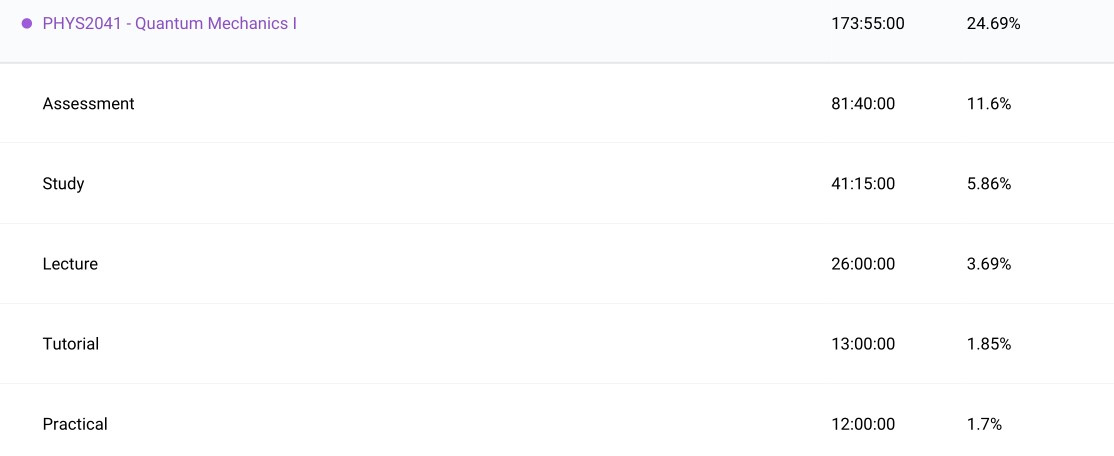
Quantum Mechanics I (PHYS2041): I have already pointed out the time I committed to learning this subject which shows the struggle physics courses go through to find a balance between theory and practice. This course follows ‘Introduction to Quantum Mechanics’ by David Griffiths very closely and I think it is a fantastic reference as a first dive into proper quantum mechanics through the wave function approach. I finally started enjoying lab sessions in this course as well; the reports were substantial and meaningful and the experiments were fun and informative to solidy understanding of quantum mechanics.
Semester 1 2024
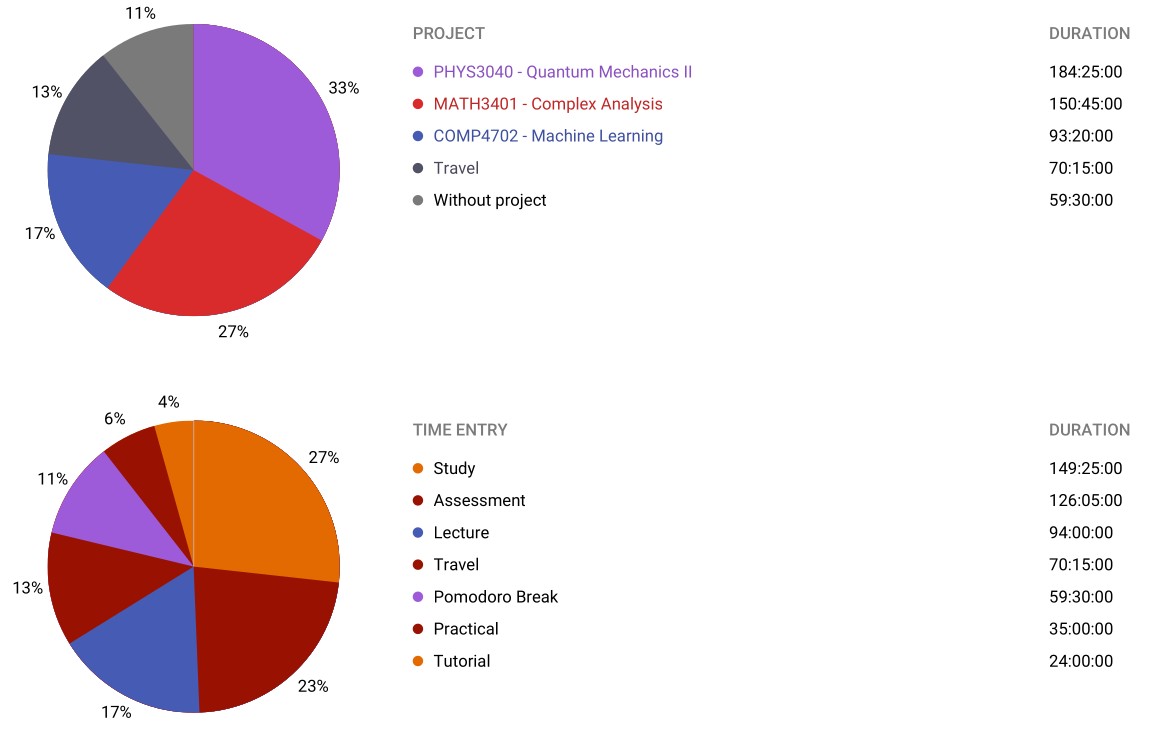 For this semester I adapted the pomodoro technique to 50/10 which I found much better in terms of productivity and I could still maintain the endurance from the 45/15 ratio. Once again the physics course exceeds the recommended guide of 10-12 hours per week. Study hours had gone up this semester fronm last despite taking one less course which is interesting.
For this semester I adapted the pomodoro technique to 50/10 which I found much better in terms of productivity and I could still maintain the endurance from the 45/15 ratio. Once again the physics course exceeds the recommended guide of 10-12 hours per week. Study hours had gone up this semester fronm last despite taking one less course which is interesting.
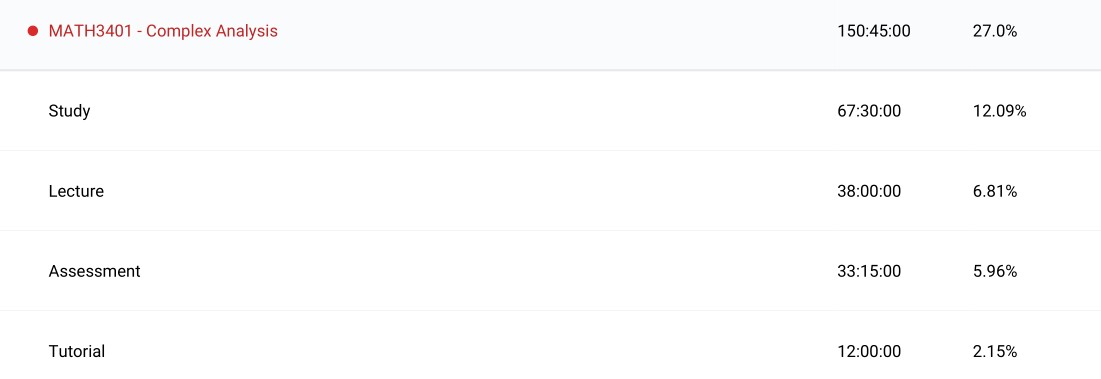
Complex Analysis (MATH3401): Mathematics on the complex plane is just so damn nice. It was such a nice change to do mathematics where everything falls into place and makes sense from one or two definitions rather than constantly running into exceptions and making up new definitions to account for said exceptions. Sure you may have to be careful when taking the logarithm but everything else works so well. ‘Complex Variables and Applications’ by James Browns and Ruel Vance Churchill was not my favourite reference but everything was clear and easy to follow.
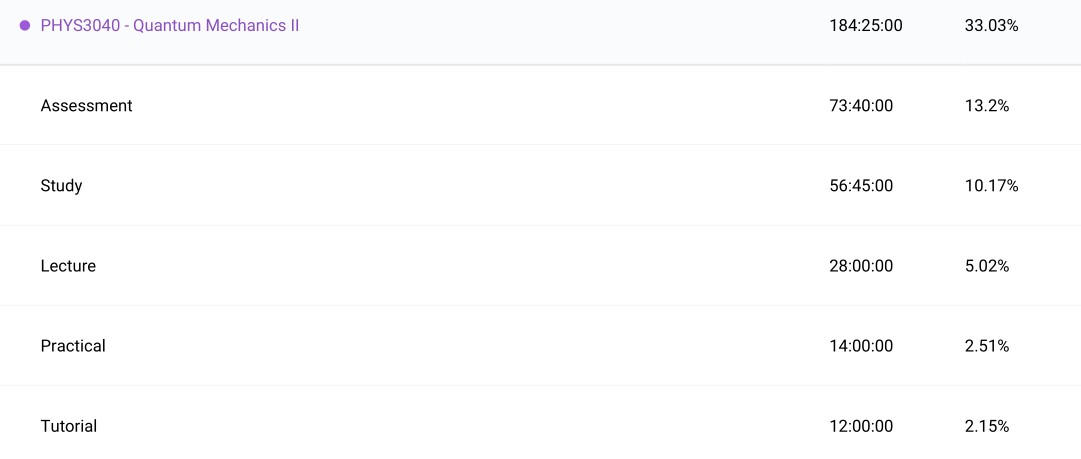
Quantum Mechanics II (PHYS3040): This was another one of my absolute favourite courses I had taken and was well worth the commitment to see out the physics minor after switching to mathematics. It was a challenging course but satisfying once things started to make sense. I also conducted some of my favourite lab experiments including the Franck-Hertz experiment and electron spin resonance. Physics experiments were a great hands-on experience for the collection process of data that was skipped over regularly in my computer science courses. MATLAB was used as the primary tool for data analysis. ‘Quantum Physics’ by Michael Le Bellac became one of my most favourite textbooks and I even revisited it briefly recently to learn about open quantum systems. I also used ‘Modern Quantum Mechanics’ by J. J. Sakurai as a supplementary reference. I would have loved to have taken functional analysis either prior to or concurrently with this course so I could truly appreciate the mathematics behind the phenomena.
Semester 2 2024
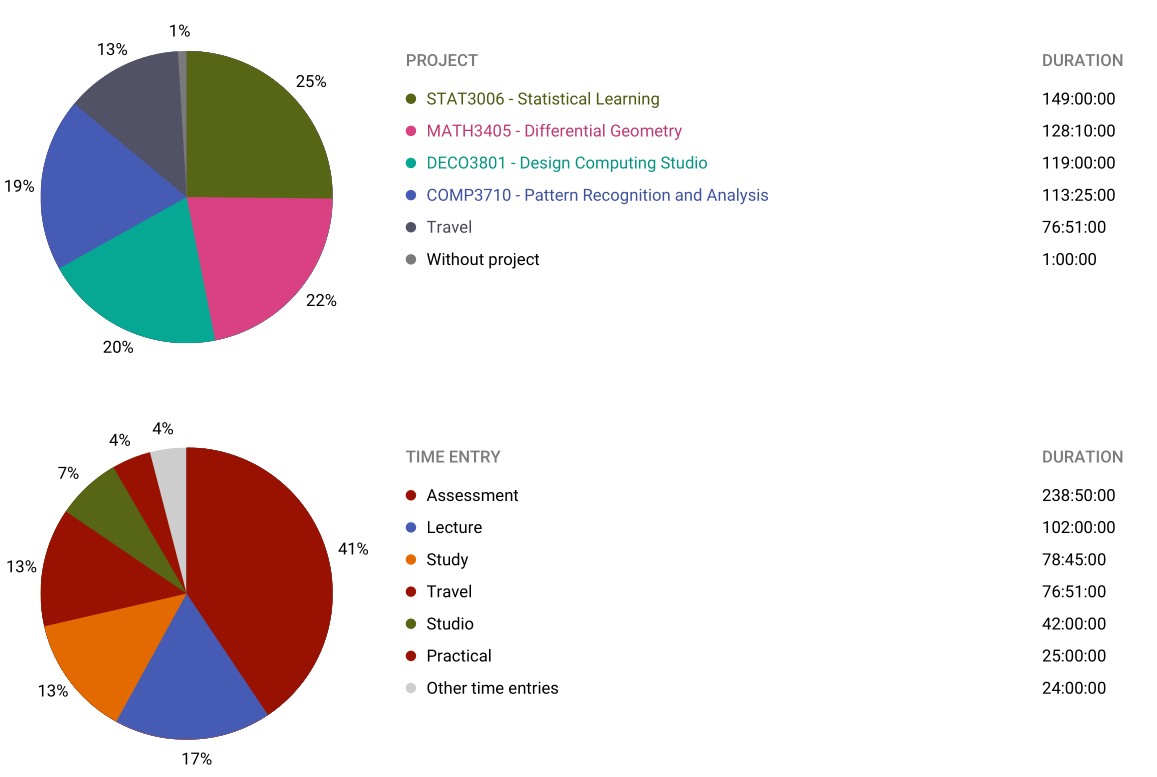 Going into this semester I made the largest and most complicated change to my study schedule largely due to a change in Toggl Track and their decision to discontinue the application for Linux distributions. I no longer stuck to a fixed schedule for my working and breaks. Instead for every 25 minutes of work I completed I added 5 minutes of break, in essence keeping the same ratio as the default 25/5. I would then take a break when I decided I was ready. It took a while for this to work because I developed the habit of I should always aim for 3-hour blocks which did not always work well. Eventually I learned that it was good to take frequent breaks, often at the 50 minute mark. This style meant that I could really do deep sessions, most useful for programming problems.
Going into this semester I made the largest and most complicated change to my study schedule largely due to a change in Toggl Track and their decision to discontinue the application for Linux distributions. I no longer stuck to a fixed schedule for my working and breaks. Instead for every 25 minutes of work I completed I added 5 minutes of break, in essence keeping the same ratio as the default 25/5. I would then take a break when I decided I was ready. It took a while for this to work because I developed the habit of I should always aim for 3-hour blocks which did not always work well. Eventually I learned that it was good to take frequent breaks, often at the 50 minute mark. This style meant that I could really do deep sessions, most useful for programming problems.
One other change is that pomodoro breaks were no longer shown as a separate time entry but rather a tag of the current project. So the pomodoro stats are shown below

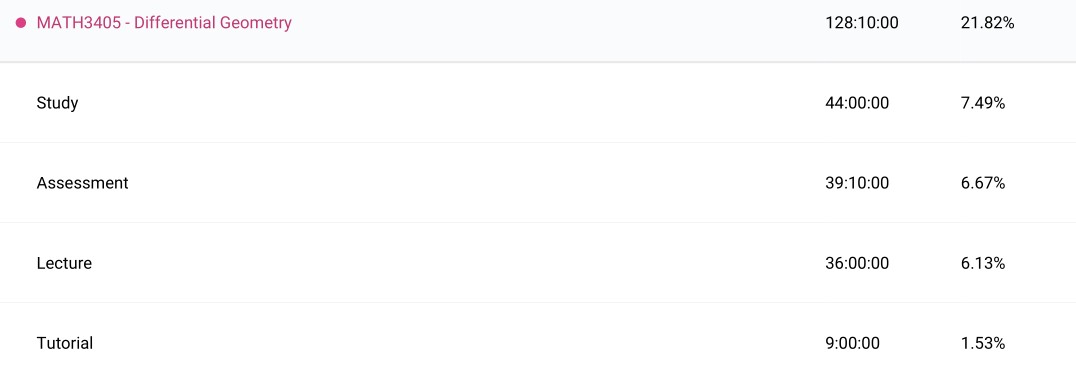
Differential Geometry (MATH3405): There were a lot of courses that I wanted to take for this math course including partial differential equations, optimisation theory and set theory. Eventually I settled on differential geometry as I heard good things about the course and I had come across some topics in the field. It was definitely a course worth taking and my mathematical physics major would be incomplete without it. The course follows Do Carmo’s ‘Differential geometry of curves and surfaces’. I was slightly dissapointed to not cover the topics of manifolds and Lie groups, but the course set me up well to be able to learn about them in my own time and I intend to.
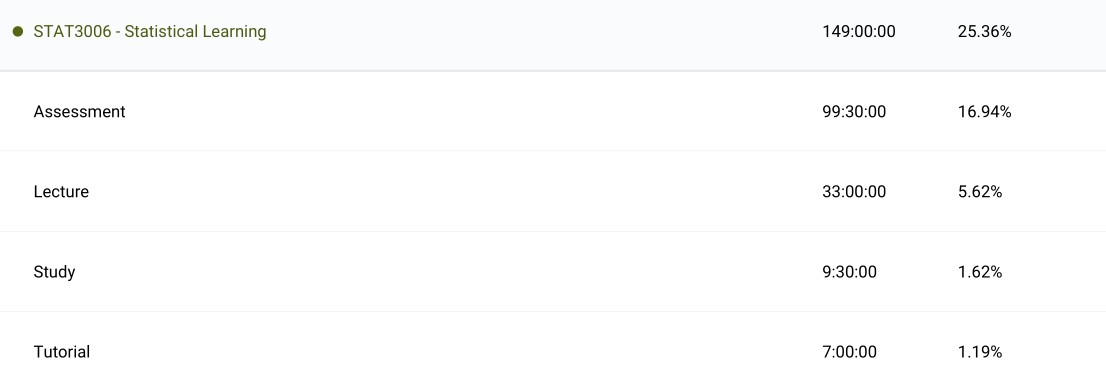
Statistical Learning (STAT3006): This course is better suited for the Computer Science section but it is a statistics course so I will talk about it here as well. I very much enjoyed this course and found it one of the most useful machine learning courses for learning about the underlying theory of the algorithms and models although I doubt I would find success without other machine learning courses as background. Hastie’s ‘The Elements of Statistical Learning’ was a fantastic resource that I can keep coming back to, although the order of models analysed, in both the course and textbook, is slightly odd to me. The highlight of the course was delving into high-dimensional statistical analysis. The course was taught using R programming language which I found to be good for doing statistical analysis and having another tool I was comfortable with. I used ‘Practical Machine Learning in R’ as the reference.
Semester 1 2025
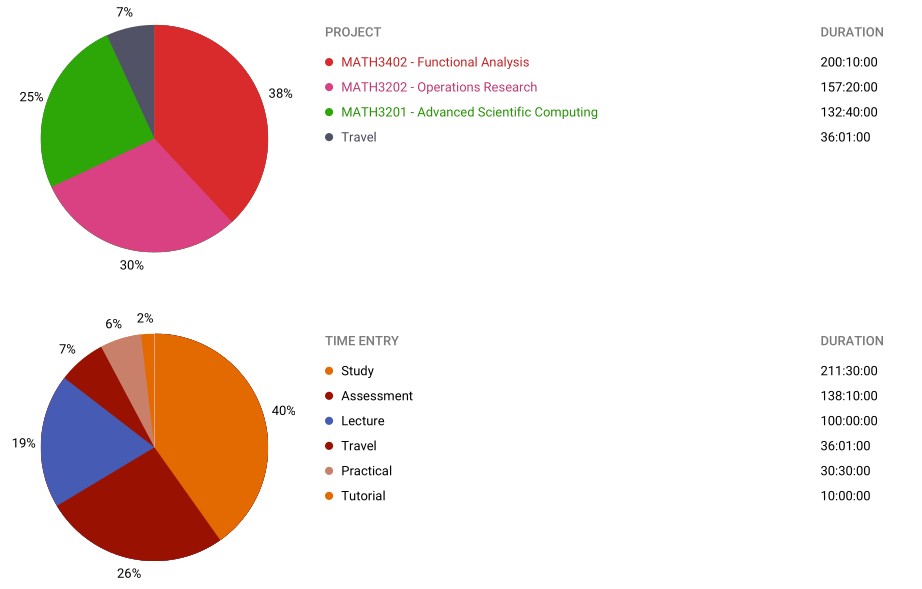 First thing to notice is I managed to get a lot of work done this semester. There was not any noticeable increase in the workload relative to other math courses in previous semesters, I think I just felt extra motivated this semester being my final and taking enjoyable and interesting courses.
First thing to notice is I managed to get a lot of work done this semester. There was not any noticeable increase in the workload relative to other math courses in previous semesters, I think I just felt extra motivated this semester being my final and taking enjoyable and interesting courses.

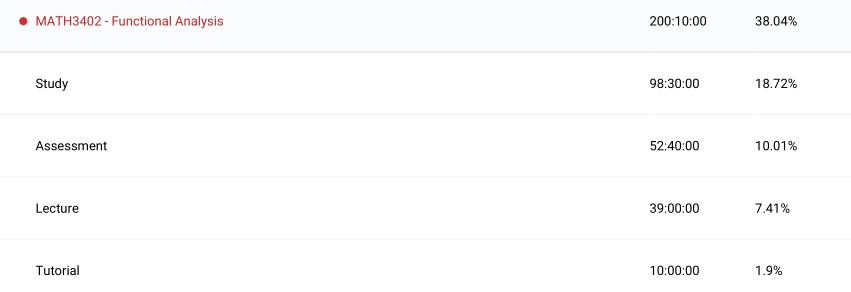
Functional Analysis (MATH3402): This ended up being a monster course in terms of total hours studied. The structure was one-third for general topology and two-thirds functional analysis. Overall, it became my absolute favourite mathematics course I took, even displacing my love for algebra courses. It is a very theory-heavy and abstract course and in my first few weeks, I nearly gave up on pure mathematics because everything just felt made up especially in topology. Since my exposure to topology was geometric results, the definitions made no sense because I kept trying to make connections with that area. Eventually everything made sense and I could appreciate the beauty in the definitions and results. James Munkres’ ‘Topology’ was a fantastic reference to turn to to get my head around these new concepts and is another one of my favourite textbooks I encountered. Similarly the functional analysis section took a lot of time before I started to understand the big ideas, theorems and results. Berezansky’s ‘Functional Analysis: Volume I’ was a good reference but I would not go back to it. At the end of the course I felt like I had a really good grasp on the content and the purpose for studying the area, better than any other course that I had taken previously. And yet I performed poorly on the final exam. I don’t want to bring up results and grades because that’s not the main point, it’s the learning and the content. But it is fresh in my mind and beyond frustrating to pour so many hours and to feel like I understand the key takeaways just to trip up in a 2-hour exam.
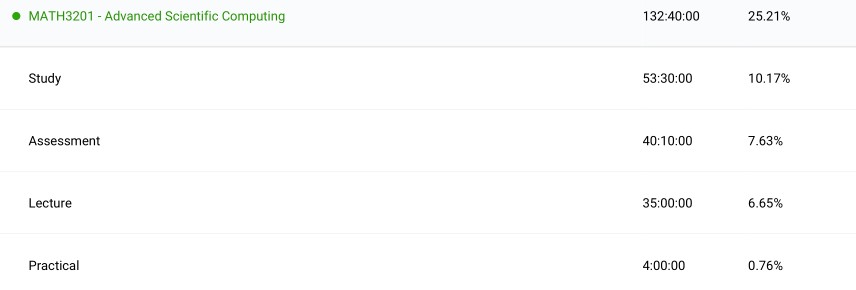
Scientific Computing: Advanced Techniques & Applications (MATH3201): This was a good course in numerical analysis. It fit in well with my passion for topics in mathematics as well as computation. I thought numerically solving partial differential equations was the main part of the course, but a wide variety of topics was covered. Timothy Sauer’s ‘Numerical Analysis’ was a good reference that I had used before briefly in a physics experiment. The course was conducted in python which suited me well.
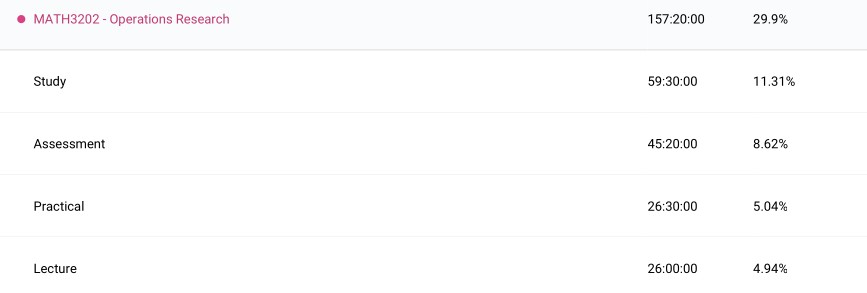
Operations Research & Mathematical Planning (MATH3202): Certainly the most applied maths course I had taken with very little theory discussed, it ran more like a computer science programming course. Topics included linear programming, (mixed) integer programming, dynamic programming and metaheuristics. It was interesting to take a course with such strong presence in industry and real-world applications outside of software engineering. I really enjoyed learning about the content and techniques to solve these kind of optimisation problems. The Gurobi Optimizer software for Python was used for these problems. I used ‘Operations Research: Applications and Algorithms’ by Wayne Winston quite often to understand the theory. The textbook is very heavy on using a wide variety of examples to aid in explanations rather than mathematical proofs. I would have preferred more mathematical explanations independent of specific examples.
Closing Remarks
Throughout my time as an undergraduate student, I found my passion in mathematics and quantum physics. In particular seeing how mathematics can be created to help describe the behaviour of physical phenomena such as Lie algebras and operators describing the motion of a particle in quantum mechanics. It became clear to me that I won’t be a pure mathematician, my proofs and general creativity are not that good. But I enjoy immensely learning about these results, why a theorem is true or false and what impacts that has. There is an infinite amount of mathematics that I do not know, but my studies and range of courses have set me up such that I can learn about these advanced topics I believe.